Introduction
Many years ago, when I was first getting into privacy and security, I wanted to see how long passwords should be in order to be secure from brute forcing. There are plenty of password strength testers already, but I wasn’t sure if they accounted for the increase of cracking speeds over time. Then, the idea came to me: What is the maximum speed for a password cracker?
The Planck Cruncher
The Planck Cruncher is a theoretical supercomputer, designed to crack passwords as fast as the laws of physics will allow. Here is how it is constructed:
Imagine a little computer that can fit in the smallest possible space in the universe: a cubic Planck length. This little computer is able to test one password every Planck time, the shortest possible unit of time. Now, fill every cubic Planck length in the observable universe with these little computers, all testing passwords at the same time, and you have constructed the Planck Cruncher!
I should note here: of course this is impossible to create. This is just a fun idea I had, to test the theoretical security of passwords. Don’t take it too seriously.
How fast is it?
First, you need to calculate how many of those little computers can fit inside the observable universe.
The diameter of the observable universe is estimated to be 8.8×10^26 meters in diameter. To calculate the cubic volume of the observable universe, you can use the equation for the volume of a sphere: 4/3*πr^3
A sphere 8.8×10^26 meters in diameter has a radius of 4.4×10^26 meters. Substitute that into the equation to get 4/3*π*(4.4×10^26)^3 which equals 3.6×10^80 cubic meters in volume.
A Planck length is approximately equal to 1.616255×10^(-35) meters. That means a cubic Planck length would have an area of 4.222111×10^(-105) cubic meters.
Divide the volume of the observable universe by the area of a cubic Planck length, and you get how many little computers make up the Planck cruncher: (3.6×10^80)/(4.222111×10^(-105)) which is approximately 8.52654×10^184 little computers. This is the exact number (rounded up):
85265403964983393378336097748259105456962168924502458604238495861430455049618543899011655543873668882698725826961915496774007125819288029139925501721769039231796606010595173836026575332
Next, you have to find out how many Planck times are in a second.
A Planck time is approximately equal to 5.391247×10^(−44) seconds. To find how many Planck times are in a second, you simply take the inverse of that to get: 1/(5.391247×10^(−44)) which is approximately equal to 1.854858×10^43 Planck times in a second.
If you multiply the number of little computers in the Planck Cruncher by the number of Planck times in a second, you find out how many passwords the Planck Cruncher can test every second: (8.52654×10^184)*(1.854858×10^43) is approximately 1.581553×10^228 passwords tested every second. The exact number is below (rounded up):
1581552541832778082294061053931661922686201706664570527082852925518538754570483301896790400140703419500140242637035837845567215262429787192831741927642510892782256238873773986538301349050212882962091805863577761872814550820473182
The complete equation is this: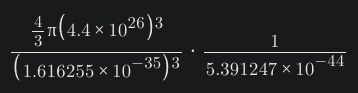 
How secure are passwords against it?
Since you know how many passwords the Planck Cruncher can test in a second, you can calculate how secure a password must be to fend it off for, say, 100 years.
There are 95 printable characters on a standard QWERTY keyboard. If you make each character of your password a randomly selected character from the 95 printable characters, you can calculate the number of possible combinations for your password using the equation 95^length where length is the length of your password. I will refer to this as the “complexity” of the password.
With that, you can calculate the bits of entropy of the password by using the equation log2(combinations) where combinations is number of possible combinations for your password. For simplicity, I will be referring to the strength of passwords by their bits of entropy. The unit used to represent entropy is the shannon unit, denoted as “Sh”.
To calculate how many seconds it would take to crack a password, you divide the password complexity by the speed of the Planck cruncher. For example:
An 8 character password has a complexity of 95^8, or approximately 6.6342×10^15. That password has an entropy of log2(6.6342×10^15), or approximately 52.56 Sh. To crack the password, assuming it was the very last password tested, the Planck cruncher would take 4.1947×10^(-213) seconds. That is orders of magnitude shorter than a Planck time itself.
So, how many bits of entropy is secure against the Planck Cruncher? If you wanted a password that is strong enough to keep the Planck Cruncher at bay for 100 years, the password would need an entropy of approximately 789.66 Sh. The password would be 121 characters in length (rounded up).
A passphrase with the same entropy (assuming 7,776 words are in the wordlist, from the EFF Large Wordlist for Passphrases) would have 62 words (rounded up).
Conclusion
Obviously if the the universe is (literally) against you, you have bigger problems than a password protecting your sensitive data. This was just a fun thought experiment to see what the upper limit of password cracking is. It’s interesting to see how a 1024 bit key would be resistant against even the fastest theoretical supercomputer for over a vigintillion years (assuming it has no other weaknesses). I hope you had as much fun reading this as I did writing it. Be sure to use strong passwords, and use a password manager.
A place to discuss privacy and freedom in the digital world.
Privacy has become a very important issue in modern society, with companies and governments constantly abusing their power, more and more people are waking up to the importance of digital privacy.
In this community everyone is welcome to post links and discuss topics related to privacy.
Some Rules
- Posting a link to a website containing tracking isn’t great, if contents of the website are behind a paywall maybe copy them into the post
- Don’t promote proprietary software
- Try to keep things on topic
- If you have a question, please try searching for previous discussions, maybe it has already been answered
- Reposts are fine, but should have at least a couple of weeks in between so that the post can reach a new audience
- Be nice :)
Related communities
Chat rooms
-
[Matrix/Element]Dead
much thanks to @gary_host_laptop for the logo design :)
- 0 users online
- 57 users / day
- 383 users / week
- 1.5K users / month
- 5.7K users / 6 months
- 1 subscriber
- 2.96K Posts
- 74.6K Comments
- Modlog
Having worked in penetration testing before, one tool I used to query SQL databases represented unknown characters as an underscore (
_) before the character gets brute forced.Bonus story: I used to set the hostname for my phone as a transparent character, so it wouldn’t visibly show up if someone ever did a network scan. I accidentally fooled myself with this while doing a network scan, and got frustrated why the “mystery device” wouldn’t load a hostname.
I feel much better knowing that my 300 entropy passwords that are like 64 characters along are pretty damn good in that case.
A password with 300 bits of entropy would take 1.288×10^(-138) seconds to crack with the Planck Cruncher :)
Good thing we don’t have a Planck Cruncher ;-)
Neat post, OP! I think I missed how is Shanon entropy relevant to the calculation. Is it relevant, or was it just a neat extra to add?
Just a neat extra. Most passwords are represented in bits of entropy in this context, and I discovered while researching that the proper unit is a shannon.
Don’t give Sam Altman ideas.
Sounds like a paperclip generator fucked the torment nexus.
Tossing around big numbers to estimate things like this is so fun, thanks for the write up!
I have a friend who absolutely hates that I only focus on theoretical problems, rather than physical problems. Oh well, I’ll be laughing when the Planck Cruncher breeches his accounts :)
The EFF wordlist does not use all 95 printable characters on the keyboard.
I don’t think that matters, since when bruteforcimg a passphrase it’s more like using whole words as the characters (or tokens) in the password. If there’s 7776 possible unique words, it doesn’t matter what characters are in the words at all. Just how many password combinations are used.
Side note, this is assuming words without character replacements. If you consider variations with A->@ or B->8 there ends up being significantly more possible unique “words”
What a fun thought experiment
Okay but what if you use emoji in your password?
I may make a writeup about this, considering a password with all possible Unicode characters instead of just the printable ASCII characters.
You’re describing the best case scenario for the person wishing to protect their password, where the Planck Cruncher guesses the password on the very last possible combination, taking 100 years to get there.
The Planck Cruncher might guess the password correctly on the first try, or it might guess correctly on the last possible combination in 100 years.
What we really want to measure are the odds of a random guess being correct.
The most “realistic” scenario is the Planck Cruncher guessing correctly somewhere between 0 and 100 years, but you want to adjust the length of the password to be secure against a powerful attack during the realistic life of whatever system you’re trying to protect.
On average, assuming the rate of password testing is constant, it’ll take the Planck Cruncher 50 years to guess the 121 character password.
And that assumes the password never changes.
If the password is changed while the Planck Cruncher is doing its thing, and it changes to something that the PC has already guessed and tested negative, the PC is screwed.
Hint: Change your password regularly.edit: The user should change their password regularly during the attack.Each password change reduces the risk of a lucky guess by that many years of PC attack.
Nope, don’t rotate passwords. Just don’t. Best case scenario, you’re wasting your time; worst case, people will actually make their passwords less secure by rotating them, e.g. some people would happily change “password123” to “password1” and call it a day.
Just pick a looong password once, make sure you don’t reuse it elsewhere, and you’ll be fine.
This is as per the NIST latest guidelines.
Tangential note: NIST has collaborated with the NSA, while denying said collaboration. Even currently, there’s suspicions about them collaborating with NSA to chose a non-safe post-quantum E2EE algorithm.
This advice is not directly related to that, this is the same advice given by security-oriented organizations all over to compensate with people being people
But DO rotate your passwords if you suspect they’ve been leaked. Or every 5-10 years probably couldn’t hurt either. The thing that has a much bigger effect is using unique passwords for every service. And if you have a password manager, resetting 1 password after a leak is trivial.
No.
In the real world having an actual high quality lengthty password is enough to deter anyone who is trying random accounts to move on for easier targets and anything that someone has physical access to, like law enforcement who confiscated something, will have an easier time bypassing the username and password process.
Changing passwords frequently leads to easier to break passwords, especially when you follow the practice of using a different one for different systems.
I understand what you’re saying, and that in the real world, bad security practices abound among average users who are likely to have passwords like “12345678” or “password”
But in this fictional scenario, my advice is directed at someone who has something valuable enough to protect behind a 121 character passphrase against a very determined adversary who has a Planck Cruncher at their disposal and is willing to run it for 100 years to crack that someone’s data.
A little extra security protocol might be worth the extra effort.
I can see how that would be unclear, and I apologize for the misunderstanding.
At that point go with a ridiculously long password to further decrease the odds of a lucky guess.
deleted by creator
deleted by creator
This article would be more interesting if it took Grover’s quantum search algorithm into account, and made some kind of physical estimate of its limits. Grover’s algorithm lets you search N items in just sqrt(N) queries.
I did consider this while writing this, but I decided to keep it simple. I’m not sure how quantum physics would behave when we’re discussing a computer that can already calculate at Planck “speed”.
is it a 1024 bit or byte key that would resist for a vigintillion years?
1024 bit. The exact number is about 3.6019×10^72 years, which is orders higher than a vigintillion.
Does the cruncher know my birthdate though :p
The Planck Cruncher has refused to comment about this. ;)
Cool. Now do quantum bits so that they’re all simultaneously calculated. Wait… don’t
A quantum computer doesn’t just calculate every possibility simultaneously, it’s much more limited. It “calculates more things at once” in some cases.
Generally speaking, some things that are hard for a regular computer are easy quantum computers. So if an encryption algorithm is based on the difficulty of those things (e.g. RSA is based on the difficulty of factoring a semiprime number), and the thing is easy for a quantum computer (e.g. factoring a semiprime), then you could defeat the algorithm with a quantum computer.
How do you protect yourself? You base the algorithm on something that is difficult for both a regular and quantum computer, that’s what post-quantum algorithms do.
But quantum computers have one last ace up their sleeve. There is a sure-fire algorithm (Grover’s algorithm) to speed up any situation where you need to find an unknown value of a known length (in this case the secret key). To keep it simple, if to find the key a traditional computer would need N steps (because there are N possible keys), a quantum computer would need just √N, which is much less. Now, this sounds massive, and it is, but if you consider that with M bits there are 2^M keys, then if you just need to check √(2^M) keys, it’s like using keys of M/2 bits, so to defend against this you just need to make the key twice as long.
Lastly, as a footnote: quantum computers can be faster than regular computers, but strictly speaking, regular computers are more powerful, that is to say they can do more things. We say that traditional computers are turing-complete, which means that they can compute anything that is computable, that is not the case for quantum computers, which means that some things (even easy things) that a computer can do, cannot be done on a quantum computer. For example, there is no way to implement regular expressions in quantum computers, it’s impossible. I know regex look difficult, but in computation theory they are among the easiest things a computer can do.
Edit: one quick addition to the paragraph about Grover’s algorithm. If a quantum computer really just tried all the solutions at once it would be much faster than that. It would be (may my professor forgive me for saying this) “like if it guessed the bits of the key one at a time and were right on the first try”, so if you had your M bits key, you would need just M steps instead of the 2^(M/2) steps of Grover’s algorithm (this is like the difference speed difference between “checking if a word is palindrome” and “calculating who will win a game of chess when using a perfect strategy”). A computer that works like that… doesn’t (and probably will never) exist. But in literature they are called non-deterministic Turing machines. They would be powerful like a regular computer (not more) but unreasonably faster.
Not sure if this is what you’re referencing, but there’s a famous quantum computer researcher named Scott Aaronson who has this at the top of his blog:
His blog is good, talks about a lot of quantum computing stuff at an accessible level
Yeah… I’m an idiot
Why not both?
You don’t need to do either. Qbits are still bounded by the laws of computation, and the planck supercomputers as described are already perfect computers with infinite bits since they can check a password of any length in a single Planck second of operation. There’s no speed advantage when going from an infinite number of things with unique states to a single thing with infinite states.
Does Lemmy have a “They did the math”? Neat thought experiment!
Cross-posted to !bestoflemmy@lemmy.world, which is probably the closest active community we’ve got
Cool idea, great writeup!